草加寺子屋は、草加市が運営する無料学習塾です。 計算問題だけでは、退屈するので、3×3魔方陣の問題を追加しました。問題は3つ。
魔方陣の問題
全て、3×3の魔方陣です。それぞれ、解は１つ求めれば良いとします。
1～9の数字を1回ずつ使って縦横斜めの合計が15になるようにマスを埋める。一般的な3×3魔方陣。(魔法陣は魔術で用いられる図)
ヒント。「3×3魔方陣の真ん中の数は５、隅は偶数に限る」
2 4 6 8 10 12 14 16 18の9つの偶数を1回ずつ使って縦横斜めの合計が30(15の倍)になるようにマスを埋める。
ヒント1。問題１の解答を利用する(易しい)。
ヒント2。10月8日の草加寺子屋の学習プリントで、以下の問題が出題されました。次の偶数を２×□の式で表しましょう。
・８ 答＝2×４ ・２０ 答＝2×１０ ・４２ 答＝2×２１1 3 5 7 9 11 13 15 17の9つの奇数を1回ずつ使って縦横斜めの合計が27になるようにマスを埋める。
ヒント1。これも、問題１の解答を利用しますが、難しい3×3魔方陣の問題です。
ヒント2。10月8日の草加寺子屋の学習プリントで、以下の問題が出題されました。次の奇数を２×□+１の式で表しましょう。
・１５ 答＝2×７＋１ ・３１ 答＝2×１５＋１
魔方陣の解答
1～9の数字を使う問題の解答の例
「3×3魔方陣の真ん中の数は５、隅は偶数に限る」についての詳しい説明は、
魔方陣の真ん中は５をプログラムで自動に解くへ
解答の例として、以下のようなものが考えられますが、対角線、上下の対称を考えると、同じです。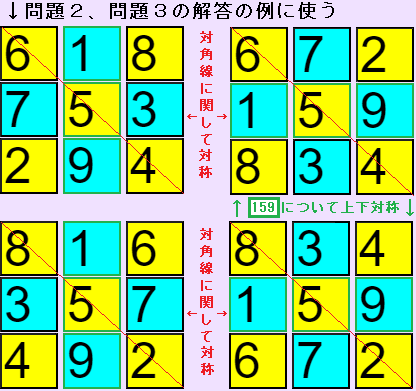
対称を除けば、3×3魔方陣の作り方は１通りです。
3×3魔方陣の作り方は何通り2～18の数字を使う問題の解答の例
問題１は、1 2 3 4 5 6 7 8 9を使いました。
問題２は、2 4 6 8 10 12 14 16 18を使います。問題１の答の数字を、全て２倍すれば、問題２の解になります。
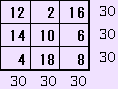
魔方陣の１列の合計が30になる理由。３列の合計＝2＋4＋6＋8＋10＋12＋14＋16＋18＝90ですから、１列の合計は30です。
３列の合計の計算は、順番を並べ替えて、
2＋4＋6＋8＋10＋12＋14＋16＋18＝
(2＋18)＋(4＋16)＋(6＋14)＋(8＋12)＋10＝
20×４＋20×0.5＝20×4.5＝90となります。
これは、結局、(最初の2＋最後の18)×(数字の個数 9)÷２という計算になります。高校数学Bで習う等差数列の和です。小学生でも高校の数学が理解できる
高校生の中で、この等差数列の和を理解できない人は、思ったよりもいます。高校では、文字(AとかX)を使って、抽象的に考えるからです。
小学生でも、具体的な数字で考えれば、なんとなく理解できると思います。具体的に理解した後なら、抽象的、厳密な説明も理解し易くなります。よって、小学生には無理だ、と考えないで、難しそうな事にチャレンジしてください。
1～17の数字を使う問題の解答の例
問題１は、1 2 3 4 5 6 7 8 9を使いました。
問題３は、1 3 5 7 9 11 13 15 17を使います。問題１の答の数字を、全て２倍して１を引けば、問題３の解になります。
１列の合計が27になる理由を考えてみましょう。