計算問題だけでは、つまらないので、新しい問題を追加しました。
素因数分解パズルの例題
下の画像の16マスに1~9の数字を入れ、横行の4個の数字の積が、右の数字と一致し、縦列の4個の数字の積が、下の数字と一致するようにします。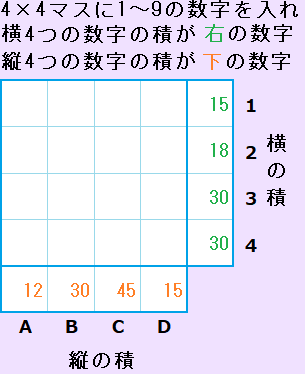
例題の答とヒント
素数は5年生で習います。素因数分解は中学1年生で習いますが、5年生でも理解できます。
素因数分解とは、ある数を素数のかけ算で表す事です。
右の数字を素因数分解。下の数字を素因数分解する。2の倍数、5の倍数は簡単に見分けられるので、この例題では、以下の素因数分解を意識しなくても、できます。
- 15=3×5
- 18=2×3×3
- 30=2×3×5
- 12=2×2×3
- 30=2×3×5
- 45=3×3×5
- 15=3×5
考え方の例。横4行の積は30(2×3×5)なので、横4行のどこかに2が入ります。しかし、縦C列、D列の積は奇数なので、2が入れるのは、A4かB4です。とりあえず、A4に2を入れます。
同じ様に横3行の積は30なので、横3行のどこかに2が入ります。2が入れるのは、A3かB3です。とりあえず、A3に2を入れます。
縦A列を考えると、A1とA2には、1と3が入ります。とりあえず、A1に1、A2に3を入れます。
横2行の積は18(偶数)なので、横2行のどこかに、2が入ります。しかし、縦C列、D列の積は奇数なので、2が入れるのは、B2です。
横1行の積は15、縦D列の積も15なので、D1に5を入れてみます。
横3行の積は30、縦B列の積も30なので、B3に5を入れてみます。同様に、横4行の積は30、縦C列の積は45なので、C4に5を入れてみます。
残りの8マスには、1、3、9が入ります。適当にやっても答に到達できます。
例題の答のうちの1つが下図です。答は、これ以外もあります。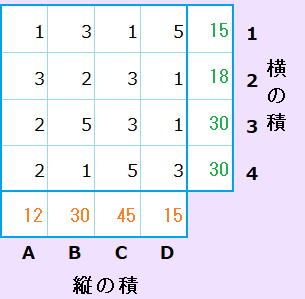
素因数分解パズルの問題1
1が使えると、答が複数 出易くなります。なので、ここからの問題は、1を使わないというルールにします。素数に1を入れない理由と関係します。
右と下にある「3557」などの数字は、525=3×5×5×7と素因数分解されるというヒントになっています。

問題1の答とヒント
この問題に対する答えは1つだけです。There is only one answer to this question.
問題1の答の緑の数字が確定する
横1行の積=525=3×5×5×7と素因数分解されます。つまり、横1行には、5が2個入るという事です。しかし、縦B列、C列の積は5の倍数ではないので、B1、C1に5は入れません。よって、A1、D1に5が入る事になります。
縦B列の積=81=3×3×3×3ですから、縦B列の4個のマスは全て3になります。よって、C1には7が入ります。
横4行の積=135は5の倍数ですから、横4行のどこかに5が入ります。しかし、C4、D4に5を入れると縦の積が合わなくなるので、A4に5が入る事になります。
問題1の答のオレンジの数字が確定する
横4行について考えます。すでに、5と3が入っているので、あと3が2個ですから、C4、D4に3が確定します。(1を使わないというルールです)
縦D列について考えます。すでに、5と3が入っているので、あと2が2個ですから、D2、D3に2が確定します。
問題1の答の赤の数字が確定する
横3行について考えます。すでに、2と3が入っているので、あと2と3が入ります。しかし、縦A列の積=350は3の倍数ではないので、A3には3は入れず、A3に2が確定し、C3に3が確定します。
残り2マスは、7と2です。
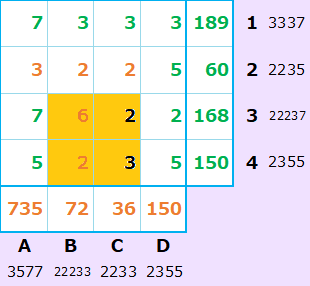
素因数分解パズルの問題2
マスの中に入れる数字は2~9です。素数ではない4や6が入っても、かまいません。
問題2の答とヒント
この問題に対する答えは2つあります。
問題2の答の緑の数字が確定する
横1行の積=189=3×3×3×7と素因数分解されます。つまり、横1行のどこかに、7があるという事です。しかし、縦B列、C列、D列の積は7の倍数ではないので、B1、C1、D1に7は入れません。よって、A1に7が入る事になります。横1行に入る残りの数字は、3個の3ですから、B1、C1、D1の3が確定します。
横3行の積=168=2×2×2×3×7と素因数分解されます。上記と同じ理由で、A3に7が入る事になります。
横4行の積=150=2×3×5×5と素因数分解されます。つまり、横4行には、5が2個入るという事です。しかし、縦B列、C列の積は5の倍数ではないので、B4、C4に5は入れません。よって、A4、D4に5が入る事になります。
縦D列について考えます。すでに、5と3が入っているので、残りは2と5です。横3行の積=168は5の倍数ではないので、D2に5、D3に2が確定します。
問題2の答のオレンジの数字が確定する
横2行について考えます。残りの数字は2と2と3です。縦A列の積は奇数なので、A2に2は入れません。よって、A2に3、B2、C2に2が入る事になります。
ここで、残ったマスは、B3、C3、B4、C4です。
B3、C3をかけると12になるので、B3、C3は、3と4か2と6です。
問題2の答 その1
B3、C3が、3と4の場合。
C3に4が入ると、縦C列の積が36になれないので、4はB3に、3はC3に入り、下図が答になります。
問題2の答 その2
B3、C3が、2と6の場合。
C3に6が入ると、C4に1が入り、マスの中に入れる数字は2~9というルールに反するので、6はB3に、2はC3に入り、下図が答になります。